Relações de contingência resposta-reforçador

por Carlos Eduardo Costa (Caê)

Ministrando uma aula no Programa de Pós-Graduação em Análise do Comportamento, na UEL, discuti com os alunos, entre outras coisas, as contingências resposta-reforçador em termos da probabilidade do reforçador dada uma resposta e a probabilidade do reforçador dada a ausência da resposta (Catania, 1998/1999, pp. 94-96). Um aluno sugeriu que eu colocasse os slides no meu site. Resolvi abordar o assunto neste post.

Contingências resposta-reforço.

Para abordar esse assunto farei uma breve introdução, do modo mais simples que eu conseguir. Espero não ser simplista ao tentar ser compreensível (para leigos em Análise do Comportamento, inclusive).

A frase de Skinner (1957), no livro Verbal Behavior, reproduzida na página inicial desse site, resume bem o modelo de seleção pelas consequências:

Os homens agem sobre o mundo e o modificam e, por sua vez, são modificados pelas consequências de sua ação.

Quando há relação entre o que fazemos e outros eventos, dizemos que há uma relação de contingência entre o que fazemos e esses eventos (uma relação de dependência entre eventos).

Relações condicionais (probabilísticas) entre as respostas e suas consequências.

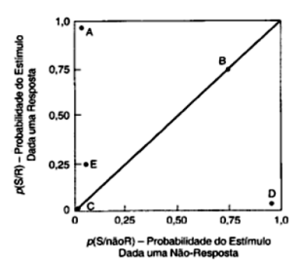
Figura 5.9. Catania (1998/1999, p. 95)

Essa relação de dependência comportamento-consequência pode ser 1:1, isto é, sempre que faço x, acontece y. Por exemplo, toda vez que aciono o interruptor, a luz se acende. Toda vez que encosto em um ferro quente, eu me queimo. Essa, e outras probabilidades, podem variar bastante. É o que Catania (1998/1999) mostra na Figura 5.9 do seu livro. O Ponto A, na figura ao lado, ilustra o último exemplo. Qual a probabilidade de y (a consequência, o estímulo reforçador) ocorrer se eu emitir a resposta (x)? Essa probabilidade é 1 ou algo próximo disso (ou, aproximadamente, 100%). Mas qual a probabilidade de y se eu não fizer x? A probabilidade é zero.

Pode existir uma relação de dependência, mas que não seja de 1:1. Algumas vezes que faço x, acontece y, mas nem sempre y acontece. Por exemplo, quando ofereço um produto para venda, eu o vendo, mas precisarei oferecer para um certo número de pessoas para que o venda. Veja, seu eu não oferecer o produto (se não faço x), eu não o vendo (não ocorre y) e, portanto, há uma relação de dependência entre x e y, mas ela não é de 1:1. Esse é o Ponto E na figura. O Ponto E ilustra um caso em que se eu fizer x, a probabilidade de y será de, digamos, 25%, mas se eu não fizer x a probabilidade de y será zero (ou próximo disso).

Fumar (x) e desenvolver um câncer de pulmão (y) é outro exemplo. Ele poderia ser, por exemplo, um Ponto F, acima de 0,75 no eixo y e abaixo de 0,25 no eixo x. Não é 100% certo que eu tenha câncer se fumar, nem é 0% a chance caso eu não fume. Mas, outros fatores mantidos constantes, é menor a probabilidade do câncer de pulmão se eu não fumar do que se eu fumar.

Pode ser que y ocorra mesmo que eu não faça x. Chamamos esses casos de eventos independentes da resposta. A probabilidade de y ocorrer é a mesma, quer eu faça ou não faça x. Essas relações cairiam na reta diagonal que corta a figura e está representada pelo Ponto B.

Pode ser que y (um dado estímulo reforçador) ocorra apenas se eu não fizer x. Por exemplo, uma criança poderia receber atenção dos pais somente se falar sem chorar. Se chorar (x) a probabilidade de atenção (y) é zero; se não chorar a probabilidade de atenção é, digamos, 100% (ou próximo disso). Esse caso estaria ilustrado no Ponto D. A probabilidade do estímulo (y) é maior se não ocorrer a resposta (x) do que se ela ocorrer. Outro exemplo seria o caso de um aluno que, se entrega o trabalho (x) nada acontece (probabilidade de y é zero); se não entrega o trabalho a probabilidade de levar uma bronca (y) é enorme! Chamaríamos este último exemplo de um caso de esquiva (um caso de comportamento mantido por reforço negativo – falarei sobre isso em outro post).

Há situações em que se eu fizer x a probabilidade de ocorrer y é zero e se eu não fizer x a probabilidade de y também é zero. Ou seja, não há nada a ser feito! Essa relação é ilustrada pelo Ponto C na figura. Chamamos isso de extinção.

Contingências resposta-reforço e os programas de reforço

A mesma figura pode identificar os programas de reforço (schedules of reinforcement). Falarei deles em outro post. Você pode conhecê-los consultando o próprio livro do Catania (1998/1999, Capítulo 10).

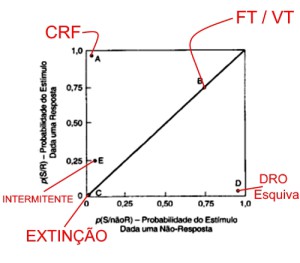
•  O Ponto A ilustra o reforço contínuo (CRF do inglês, continuous reinforcement);
• O Ponto B ilustra os programas de tempo fixo (FT do inglês Fixed Time) e tempo variável (VT do inglês Variable Time);
• O Ponto C é um caso de Extinção;
• O Ponto D ilustra um programa de reforço diferencial de outros comportamentos (DRO do inglês Differential Reinforcement of Other responses) ou de esquiva.
• O Ponto E ilustra um caso de reforço intermitente.

Cada programa de reforço intermitente poderia, dado seus parâmetros, ser identificado em um ponto específico dessa figura.

Considerações Finais

É importante ter claro que, as relações resposta-reforçador (ou resposta-estímulo) sempre são parte de uma contingência de três termos. Em outras palavras, as probabilidades condicionais podem ser afetadas pela presença de outros eventos. Por exemplo, a probabilidade do comportamento x de uma criança ser reforçado (y) pela atenção do pai, pode depender de o pai estar lendo o jornal ou fazendo outra coisa.

Portanto, entender e observar com atenção essas relações de contingência resposta-reforço é apenas um dos passos a ser dado para uma boa análise funcional do comportamento.

A descrição dessas  relações condicionais probabilísticas, feitas por Catania, é interessante porque chama a atenção para o fato de que devemos não apenas avaliar a probabilidade de um evento (reforçador ou aversivo) ocorrer quando uma resposta ocorre, mas também temos de levar em conta a probabilidade desse evento (reforçador ou aversivo) ocorrer na ausência da resposta!

Uma boa análise funcional dependerá ainda de outras coisas: especificar bem o comportamento que se quer avaliar; identificar os eventos que têm a função reforçadora para aquele comportamento (daquela pessoa, claro) e identificar as relações de contingência entre (a) os eventos antecedentes, (b) o comportamento propriamente dito e (c) as consequências.

Aqui tratei apenas da questão das relações entre (b) e (c).